
중학교 수학에서 갑자기 등장하는 것이 두 가지가 있어요. 하나는 문자, 또하나는 절댓값 기호예요.
이 두 가지가 연산을 어렵게 만드는 양대산맥이라고 할 수 있는데요, 특히 절댓값 기호는 잘못 가르치는 사람들이 많아서 아이들이 정확한 개념을 모르고 학습을 하다가 수포자의 길로 가는 경우가 많아요. 그래서 정확한 개념의 뜻을 알고 공부할 수 있는 것을 목표로 공부해볼게요.
절댓값의 정의(뜻)
절댓값이란 어떤 수를 수직선 위의 점으로 대응시켰을 때, 원점으로부터 그 점까지의 거리예요.
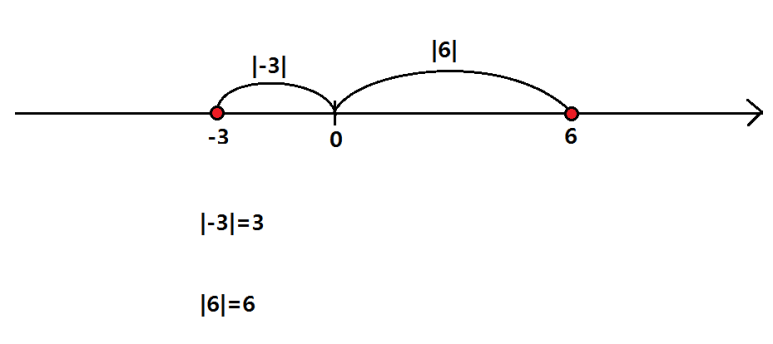
만일 -3과 6이라는 수가 수직선 상에 놓여져있는 경우라면 절댓값 -3은 원점으로부터의 거리가 3이고 절댓값 6은 원점으로부터의 거리가 6이에요..
그래서절댓값 기호가 포함된 문제를 풀다보니 세 가지 유형으로 나누어서 생각하기 시작한거에요.
음수면 양수로
양수면 그대로
0은 0
절댓값에 대한 잘못된 개념
그런데 많은 학생들이 절댓값을 |-3|에서 -부호가 없어져서 3이 된다고 잘못 알고 있어요. 그래서 절댓값의 정의는 무시하고 그냥 음수면 -를 없앤다로만 대입해서 문제를 푸는거죠. 이렇게 풀면 절대 안돼요. 그러면 쉬운 문제는 풀 수 있어요. 하지만 어려운 문제는 해석을 못하게 되는거에요.
절댓값 기호안에 -부호가 있으면
-부호를 없애버린다(X)
는 잘못된 개념이에요.
절댓값 기호 안의 수 전체가 음수이면 양수(거리개념)로 만들기 위해 -부호를 하나 더 붙인다(O)
가 맞아요.
예를 들면, -부호가 있으면 무조건 떼어내면 양수라고 생각하는 학생이 있다고 해볼게요.
|-a|
그 학생은 이 식을 보면서 이렇게 풀거에요.
'어? -부호가 있네. 그럼 -를 없애면 되겠구나'
|-a|=a

이 풀이가 맞을까요? 땡! 아니죠. -a가 양수인지 음수인지를 조사를 해야죠.
네? -a는 음수가 아닌가요? 네, 그렇게 판단하면 안돼요.
왜냐하면 a가 양수인지 음수인지 모르기 때문이에요.
a가 양수이면 -a는 음수이지만
a가 음수이면 -a는 양수랍니다.
그러니 a가 양수인지 음수인지 확인을 해야되는 거에요.
예를 들어, a=-4라고 해볼게요. 그러면 -a=-(-4)=4 와 같이 -a는 양수인거죠.
따라서 a가 음수이면 -a는 양수이므로
|-a|=-a
가 되는거에요. 절댓값 기호는 양수는 이미 거리로써 양수이니, 그대로 빠져나오는 거에요.
절댓값은 거리다.
절댓값은 거리 개념이에요. 거리가 음수가 나올 수가 없죠? 그렇기 때문에 음수인 경우 -를 붙여서 양수로 만드는 거랍니다. 따라서 절댓값 기호가 있는 문자는 다음과 같이 공식화할 수 있어요.

절댓값 기호는
"널 반드시 거리로 만들거야" , "널 반드시 음수가 되지 않게 할거야"
라는 의지의 표현이에요. 따라서 음수에게는
"넌 음수구나. - 부호를 받아. 그러면 양수가 될테니"
라고 -부호를 하나 더 주는거에요. 그러면 -5와 같은 음수는

이렇게 양수가 되는거에요. 그럼 이미 양수인 경우는


이 식은 어떻게 될까요? a+b가 양수인지 음수인지는 a의 값과 b의 값에 따라 달라져요.
만약 a=5, b=-4 이면 a+b=5-4=1 양수죠. 그러면

만약 a=-5, b=3 이면 a+b=-2이므로 음수죠. 그러면,
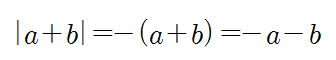
이와 같이 절댓값 기호는 음수는 -부호를 없애면 된다가 아닌,
음수이면 -부호를 붙여 양수로 만들어준다는 개념으로 아시길 바래요.
