중등 1학년 수학 > 정비례와 반비례 > 정비례와 반비례의 개념과 그래프 연습문제 프린트 학습지
정비례
$x$의 값이 $2$배, $3$배, $4$배, $\cdots$일 때, $y$의 값도 $2$배, $3$배, $4$배, $\cdots$가 되는 관계 또는 관계식입니다.
정비례처럼 보이지만 정비례가 아닌 경우는 $x$의 값이 증가할 때, $y$의 값이 증가하지만 정확히 '정'비례하지 않은 경우입니다. 가령, $x$의 값이 $2$배, $3$배, $4$배가 될 때, $y$의 값이 $4$배, $9$배, $16$배와 같이 제곱을 한만큼 늘어나면, 둘다 증가하지만, '정'비례는 아닙니다.
반비례
$x$의 값이 $2$배, $3$배, $4$배, $\cdots$일 때, $y$의 값도 $\dfrac{1}{2}$배, $\dfrac{1}{3}$배, $\dfrac{1}{4}$배, $\cdots$가 되는 관계 또는 관계식입니다.
반비례는 $x$의 증가율과 $y$의 증가율의 값을 곱하면 항상 $1$이 되는 비율관계입니다. 위에서 보는 것처럼 $x$가 2배 증가하면 $y$는 $\dfrac{1}{2}$배 증가하므로 곱하면 $1$이고, $x$가 3배 증가하면 $y$는 $\dfrac{1}{3}$증가하므로 곱하면 마찬가지로 $1$이 됩니다.
정비례 관계식
$y=ax\ (a≠0)$
정비례 관계식은 위와 같은 형태를 말하며, 예를 들면, $y=x$, $y=3x$, $y=-x$, $y=\dfrac{1}{3}x$ 등이 있습니다. 이때 체크할 부분은 $x$가 나란히 곱해진다는 것입니다. 만약 $y=\dfrac{x}{3}$가 있다면 정비례가 맞습니다. 왜냐하면 $y=\dfrac{x}{3}=\dfrac{1}{3}\times{x}=\dfrac{1}{3}x$와 같이 변형할 수 있기 때문입니다. 반면 $\dfrac{3}{x}$은 정비례가 아닙니다. 왜냐하면 $x$가 분모에 있기 때문입니다. 정리하면 분수모양에 $x$가 있을 때에는 분자에 $x$가 있어야 됩니다.
반비례 관계식
$y=\dfrac{a}{x}$
반비례 관계식은 분모자리에 $x$가 있다는 것이 특징입니다. 양변에 $x$를 곱하게 되면, $xy=a$와 같은 모양이 되는데 이것도 반비례 관계식의 변형식 중 하나라는 것도 체크하시기 바랍니다. $x$와 $y$의 곱이 일정한 값($a$)을 가진다고 하면 반비례 관계식입니다.
정비례 그래프
정비례 그래프는 $y=ax$를 만족하는 순서쌍 $(x,y)$의 점들을 좌표평면에 표시한 것입니다. 정비례 그래프는 원점을 지나는 직선 모양인데요, 정비례 그래프가 반드시 원점을 지나는 이유는 바로 $x=0,\ y=0$을 식에 대입하면 반드시 성립하기 때문입니다. ($y=ax$에 $x=0,\ y=0$을 대입하면 $0=a\times{0}$ 성립)
$a$의 값은 기울기를 나타내고, $a$가 양수이면 오른쪽 위를 향하는 그래프, $a$가 음수이면 오른쪽 아래를 향하는 그래프가 되며, $a$의 절댓값의 크기가 클수록 기울기는 가파릅니다.(또는 $y$축에 가까워집니다.)
반비례 그래프
반비례 그래프는 $y=\dfrac{a}{x}$를 만족하는 순서쌍 $(x,y)$의 점들을 좌표평면에 표시한 것입니다.
반비례 그래프는 원점 대칭인 쌍곡선 모양을 가지며, $a$가 양수이면 제1, 3사분면을, $a$가 음수이면 제 2, 4사분면을 지납니다. 쌍곡선 그래프는 $x$축과 $y$축에 한없이 가까이 다가가는데요, $x$축과 $y$축을 점차적으로 근접하는 선이라고 하여 점근선이라 부릅니다.
그럼 정비례와 반비례 연습문제를 몇 개 풀어보도록 하겠습니다.
문제1)
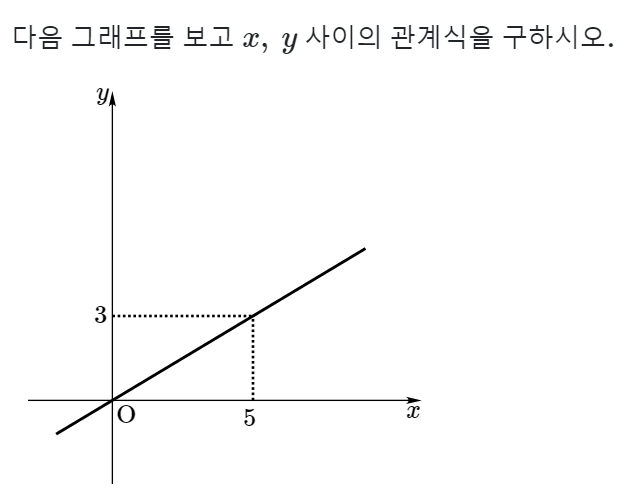
원점을 지나는 직선이므로 '정비례 관계식'입니다. $y=ax$라고 일단 식을 세운 다음 $(5,3)$에 해당하는 점을 지나므로 $x=5,\ y=3$을 정비례 관계식에 대입합니다.
$3=a\times{5}$
$a=\dfrac{3}{5}$
이렇게 구한 $a$의 값을 $y=ax$에 대입하여 정비례관계식을 완성시키면
$y=\dfrac{3}{5}x$
입니다.
문제2)

제 2, 4사분면을 지나는 원점에 대칭인 쌍곡선이므로 '반비례 관계식'입니다. 반비례 관계식은 $y=\dfrac{a}{x}$라고 먼저 식을 세운 다음, 곡선이 지나는 점(=곡선 위의 점)을 식에 대입하며 미지수 $a$의 값을 구합니다.
위 그래프에서는 $(5,-1)$과 $(-5,1)$을 지나는 정보가 있으므로 두 점 중 아무 점이나 대입합니다.
$x=5,\ y=-1$을 반비례 관계식 $y=\dfrac{a}{x}$에 대입하면,
$-1=\dfrac{a}{5}$
$a=-5$
이렇게 구한 $a$의 값을 원래 식에 대입하면 반비례 관계식이 완성됩니다.
$y=\dfrac{-5}{x}=-\dfrac{5}{x}$
이렇게 하여 정비례와 반비례 관계에 대한 개념를 학습하고 연습문제를 풀어보았습니다.
더 많은 연습문제를 풀고 싶은 분께 '모두매쓰' 사이트를 추천드립니다.
모두매쓰는 수학 문제를 무제한으로 생성하여 프린트할 수 있는 학습 사이트입니다.
위에서 제시한 연습문제는 모두매쓰에서 생성한 문제입니다.
[모두매쓰 생성 연습문제]
중등 1학년 수학 > 정비례와 반비례 > 정비례와 반비례의 개념과 그래프 연습문제 프린트 학습지