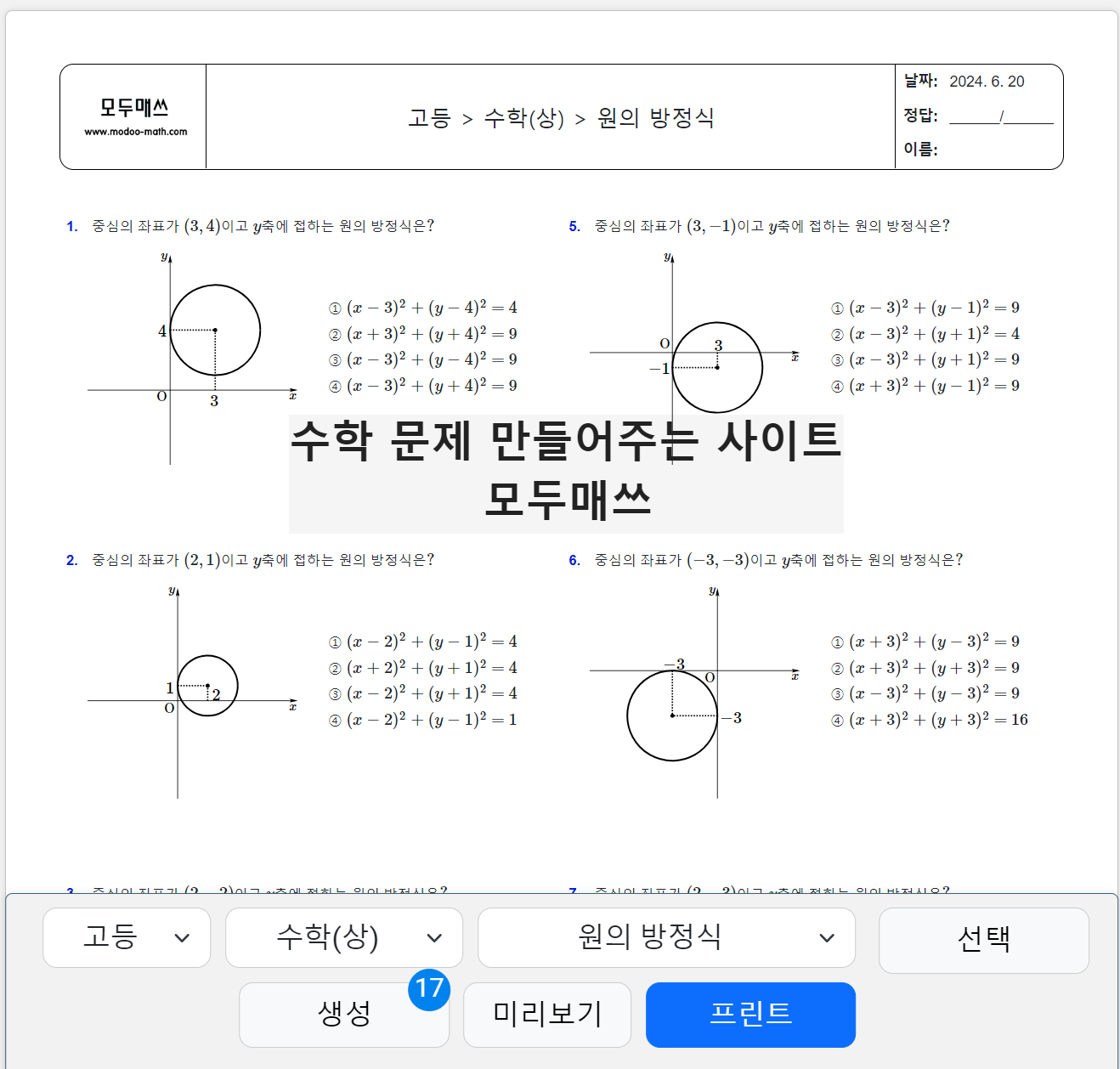
수학(상) > 도형의 방정식 > 원의 방정식이 만들어진 원리, 연습문제 프린트 학습
원의 방정식
중심 (a,b), 반지름 r인 원의 방정식은
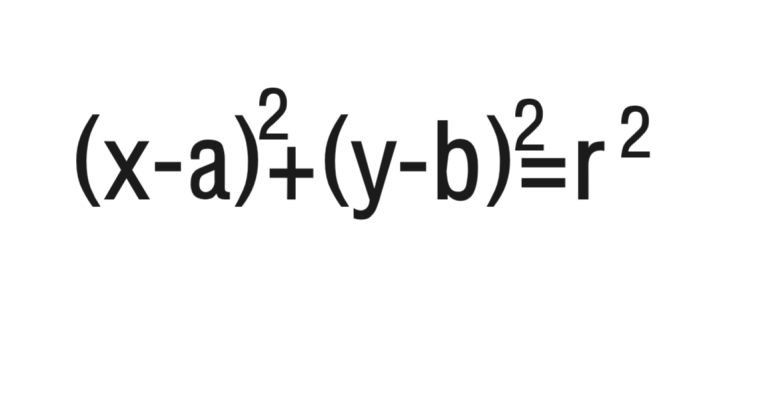
와 같아요. 원의 방정식은 왜 위와 같은 모양을 가지게 되었는지 설명하려면 원의 정의와 피타고라스의 정리가 필요해요.

원의 정의
고정된 점을 기준으로 같은 거리에 있는 점들의 자취(모임)
이 정의에 따라 위 그림에서 고정된 점 (a,b)을 기준으로 일정한 거리 r만큼 떨어진 점 (x,y)가 있다고 하면,
(x,y)는 무수히 많은 점들이 가능해요.
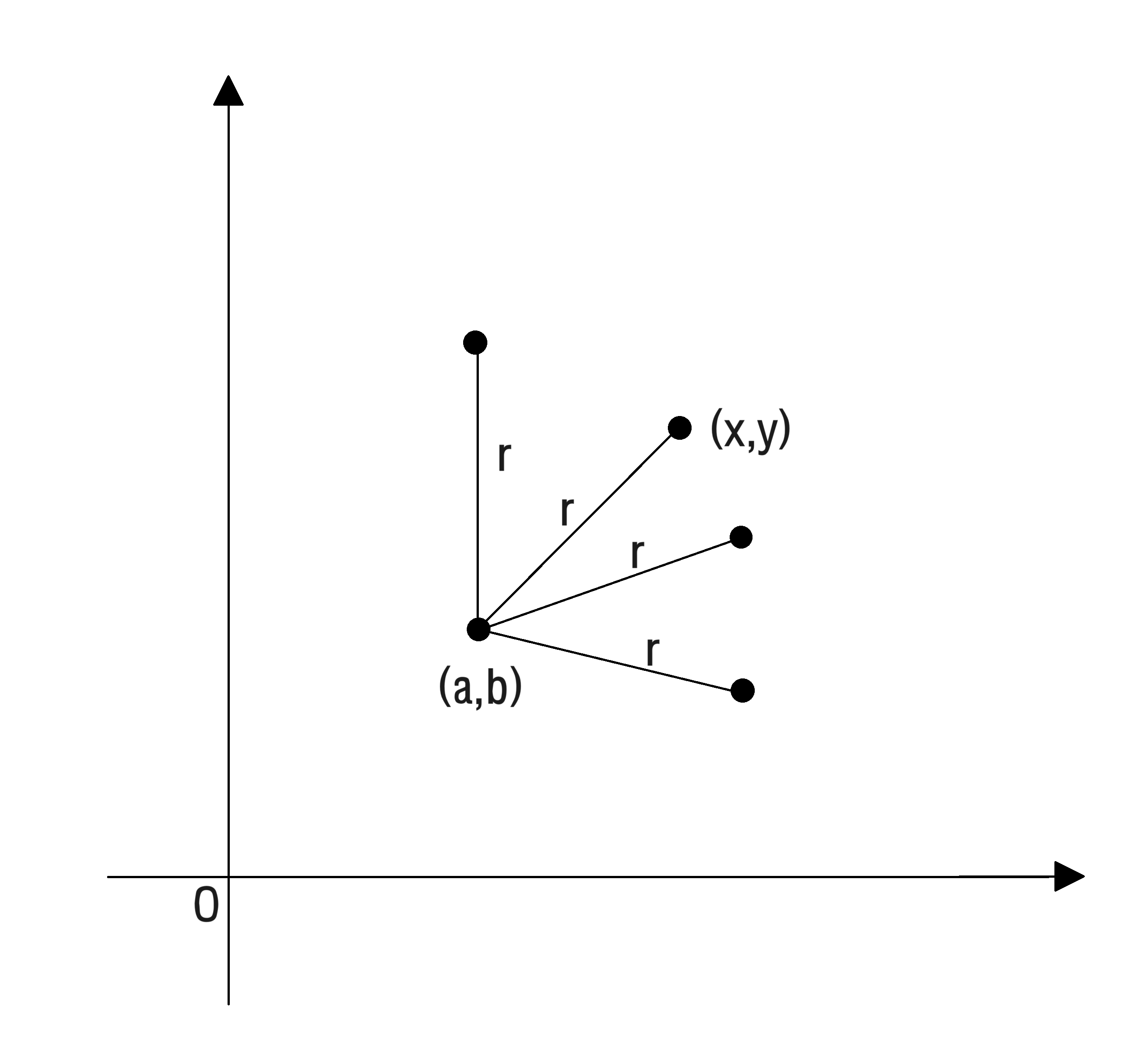
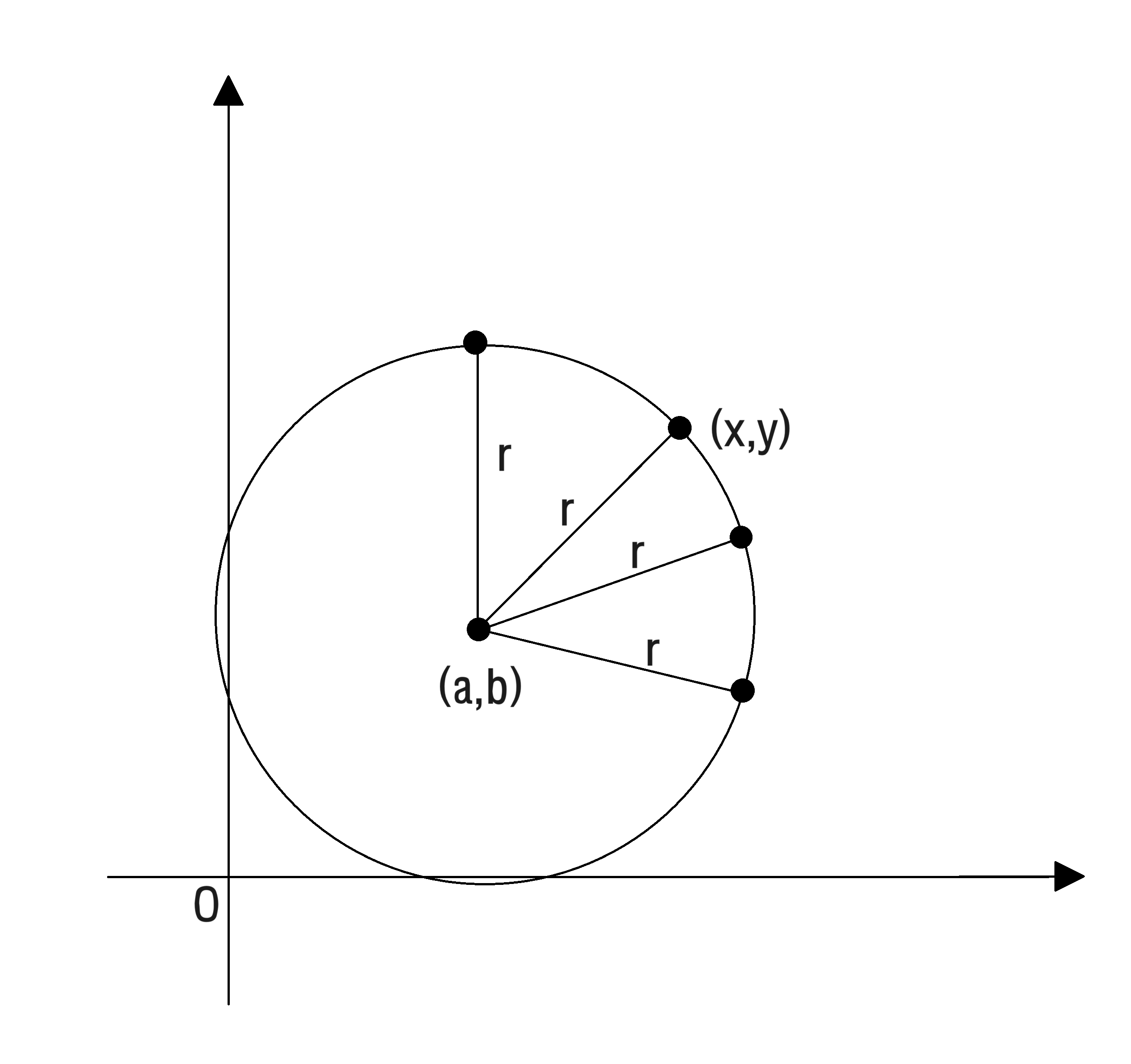
원의 정의에 따라서 무수히 많은 (x,y) 점들을 표현할 수 있는 식이 필요하게 되었어요.
여기에서 피타고라스의 정리가 사용됩니다

. 피타고라스의 정리를 사용하려면 아래변과 높이를 길이로 나타낼 수 있어야해요. 이때 좌표평면의 좌표가 큰 역할을 해요.

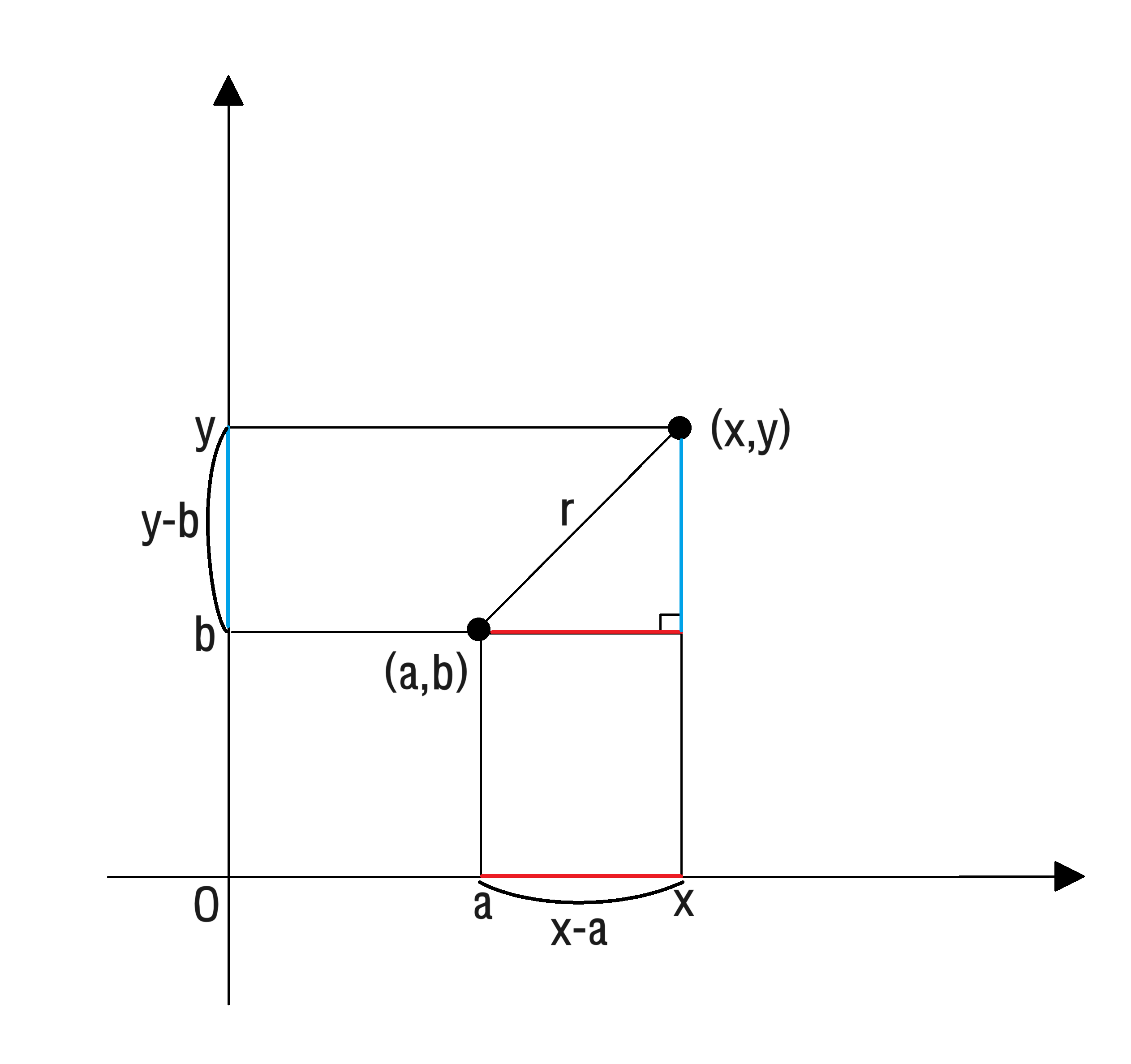
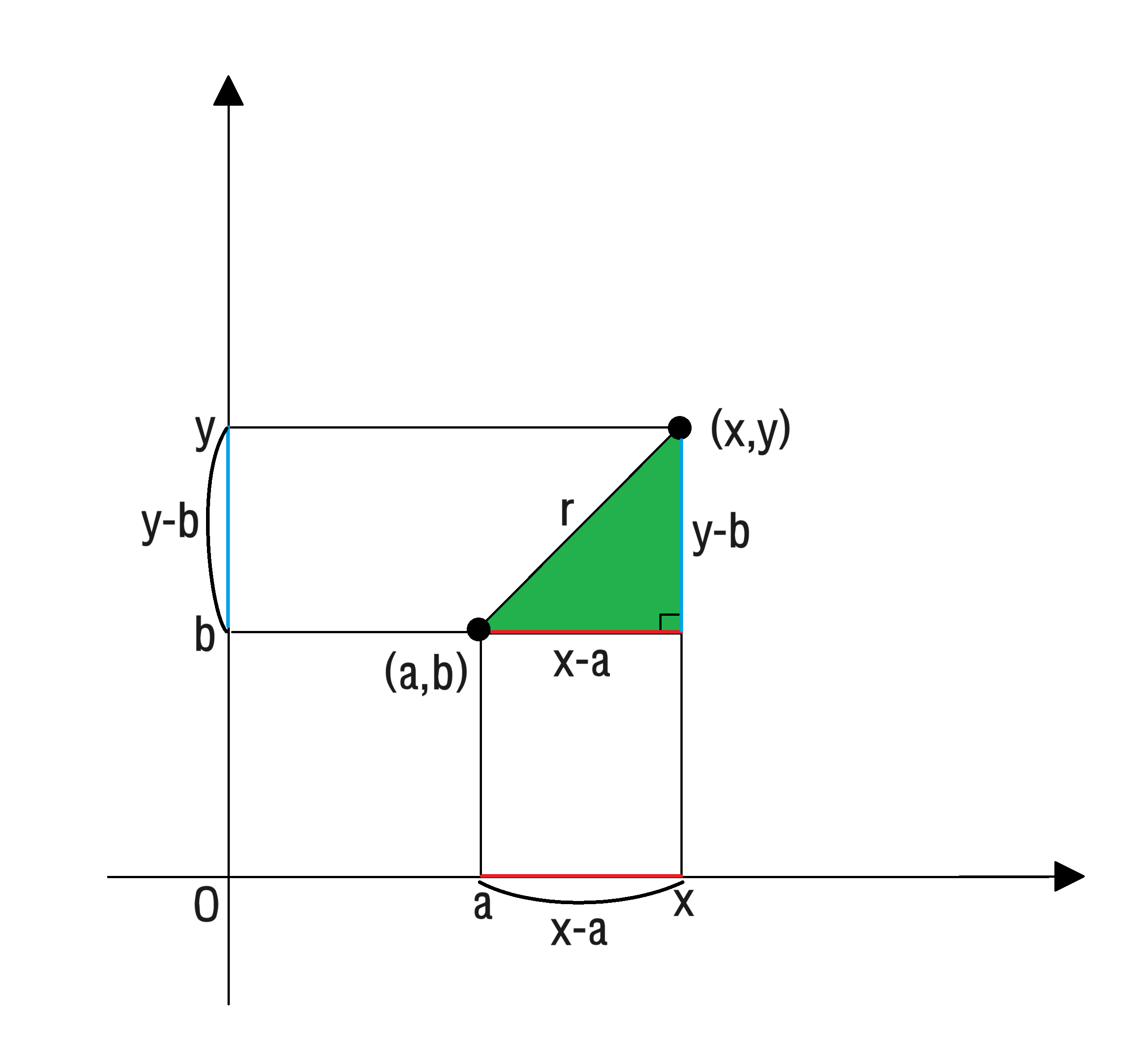
피타고라스 정리를 이용하여 나타내면 다음과 같습니다.
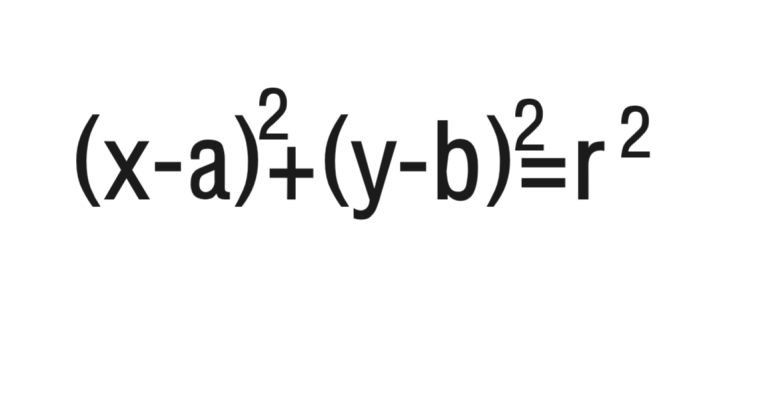
이게 바로 원의 방정식이에요. 이 식을 만족하는 (x,y)점은 원 위의 점이고, 그러한 점들을 모두 모으면 원 모양의 그래프가 됩니다.

이렇게 원의 방정식이 만들어지는 과정에 대해서 살펴보았는데요,
원의 방정식은 원의 정의와 피타고라스의 정리, 그리고 좌표평면의 도움을 받게 되어 탄생하였다는 것을 알면 왜 방정식의 모양이 저런 모양이 될 수 밖에 없는지 더욱 잘 이해할 수 있게 된답니다.
관련된 문제를 하나 풀어보도록 할게요.
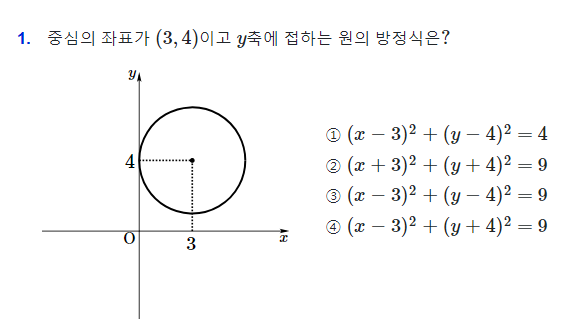
그래프의 중심이 (3,4)이고 반지름은 중심의 x좌표와 같으므로 3이에요.
따라서 정답은 3번이 됩니다.
지금까지 원의 방정식이 만들어지는 과정과 원리를 설명하고, 문제를 하나 풀어봤습니다.
같은 문제를 계속해서 생성해주는 수학 학습지 사이트 '모두매쓰'에서 더 많은 연습을 하길 바래요.
수학(상) > 도형의 방정식 > 원의 방정식이 만들어진 원리, 연습문제 프린트 학습
'중등 수학 프린트' 카테고리의 다른 글
| 중등 3학년 수학 > 대푯값과 산포도 > 표준편차 공식, 연습문제 프린트 학습지 (0) | 2024.07.12 |
|---|---|
| 중등 3학년 수학 > 대푯값과 산포도 > 분산 공식, 연습문제 프린트 학습지 (0) | 2024.07.12 |
| 중등 3학년 수학 > 대푯값과 산포도 > 편차의 개념과 성질, 연습문제 프린트 학습지 (0) | 2024.07.12 |
| 중등 1학년 수학 > 엇각 쉽게 찾는 2가지 방법, 연습문제 프린트 학습지 (0) | 2024.07.12 |
| 중등 2학년 수학 > 도형의 닮음 > 평행선 사이의 선분의 길이의 비 개념, 연습문제 프린트 학습지 (0) | 2024.07.12 |