고등 수학II > 도함수의 활용 > 사차함수의 최댓값과 최솟값 구하기 연습문제 프린트 학습지
사차함수의 그래프를 그릴 수 있으면 최댓값과 최솟값을 구하는 문제도 동시에 해결이 되는데요,
사차함수의 그래프의 개형에 대해 알아보고 위 함수 $f(x)$의 그래프를 그려보도로 할게요.
사차함수의 개형
사차함수의 개형은 크게 4가지가 있습니다. 그 기준은 사차함수 $f(x)$를 미분한 $f'(x)$이 $x$축과 만나는 점이 몇 개인지에 달려있어요.
$f'(x)=0$ 방정식의 해의 종류 → 사차함수의 개형 4가지를 결정
사차함수를 미분한 함수 $y=f'(x)$는 삼차함수이고, $f'(x)=0$은 삼차방정식이에요.
개형을 하나씩 살펴보도록 할게요.
사차함수의 개형1)
$f'(x)=0$이 서로 다른 세 실근을 가질 때,

사차함수의 개형2)
$f'(x)=0$이 한 실근과 한 중근을 가질 때,

사차함수의 개형3)
$f'(x)=0$이 한 실근과 두 허근을 가질 때,
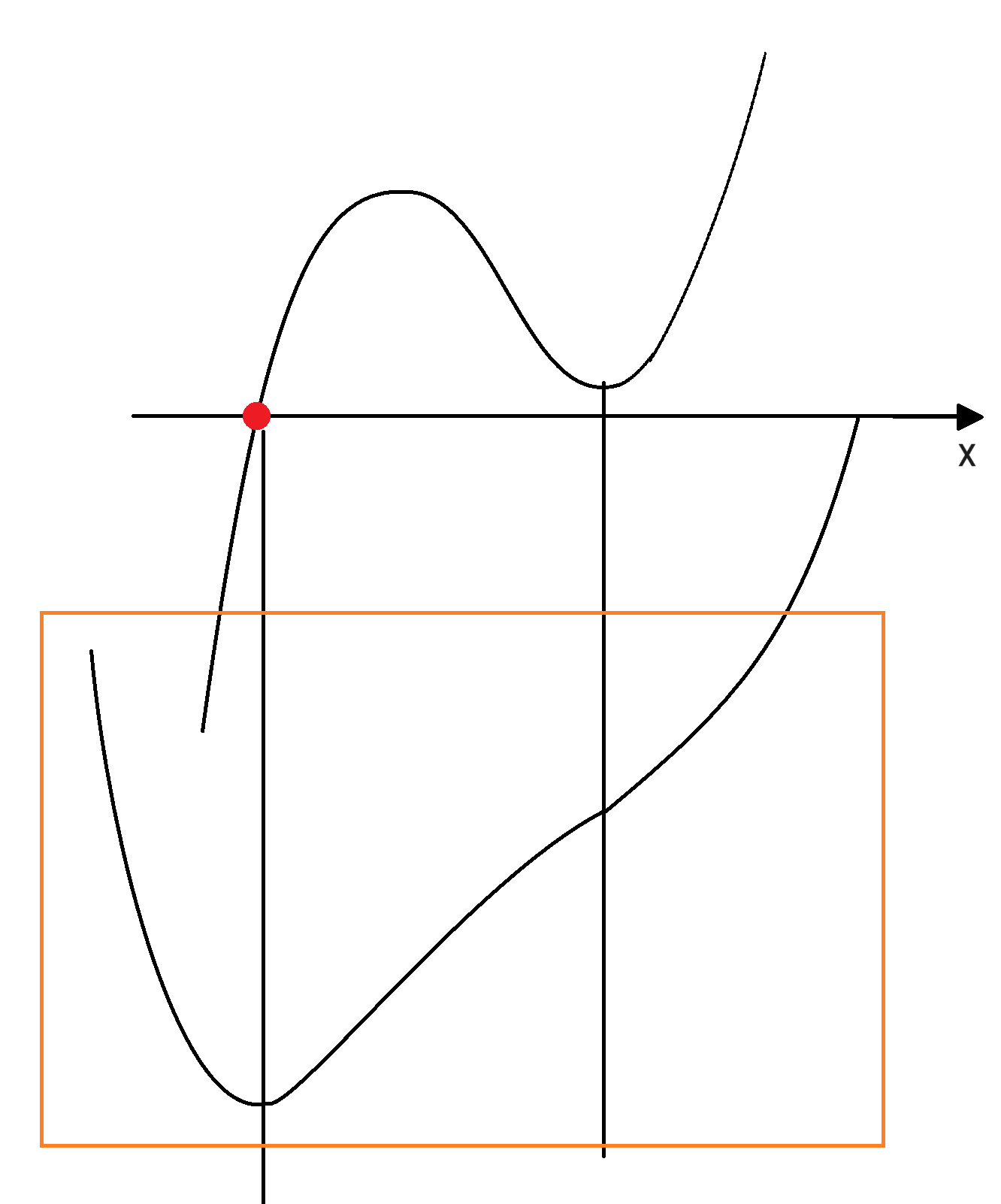
사차함수의 개형4)
$f'(x)=0$이 삼중근을 가질 때,(=서로 같은 세 실근을 가질 때)

이렇게 해서 사차함수의 그래프 개형이 4가지인 것을 확인했구요,
문제를 풀어보도록 하겠습니다.
문제)

풀이)
함수의 그래프 개형을 찾으려면 $f'(x)=0$이 되는 $x$의 종류는 알아야합니다.
$f'(x)=-4x^3+4x=0$
$-4x(x^2-1)=0$
$-4x(x+1)(x-1)=0$
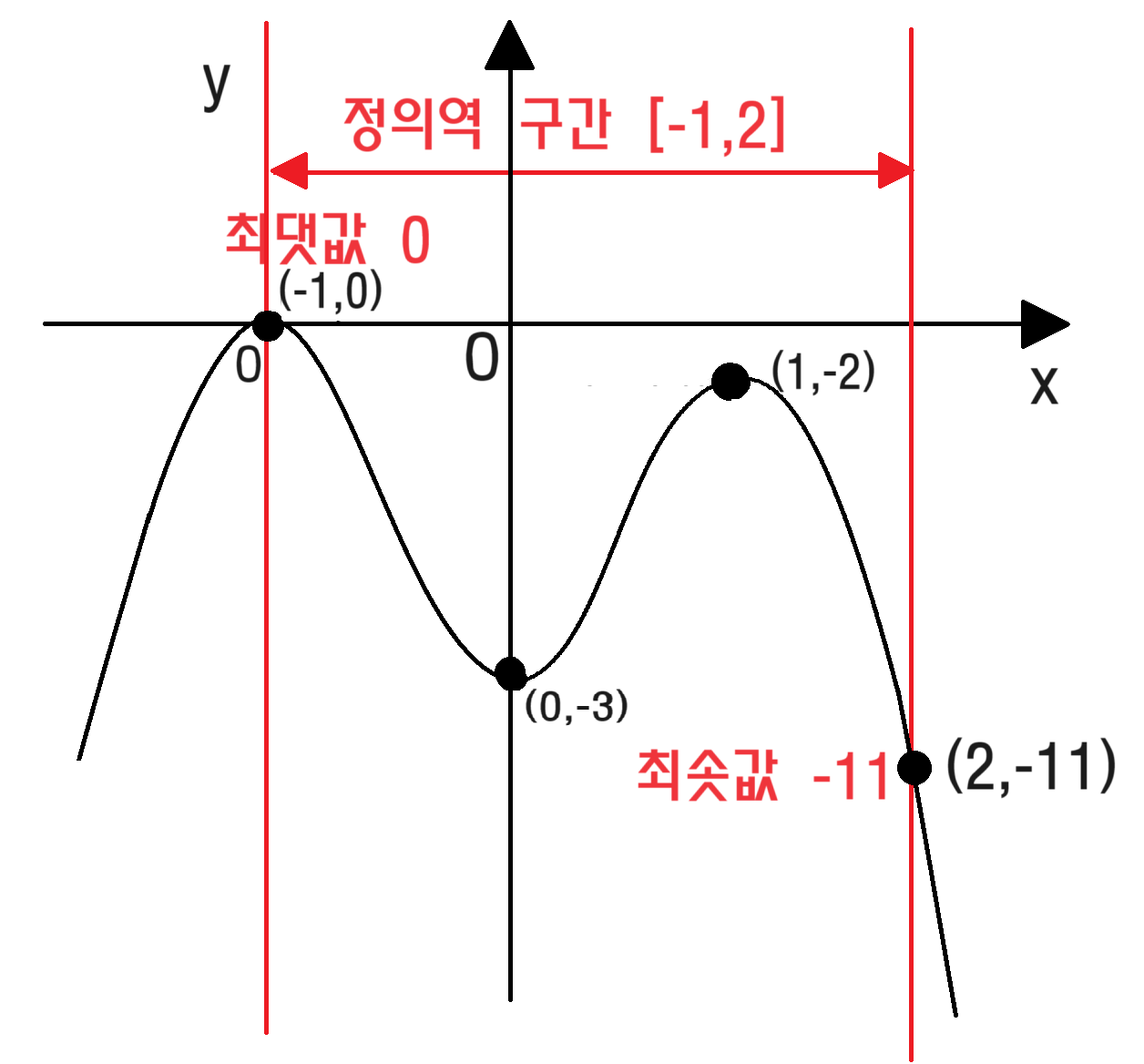
따라서 $x=-1$ 또는 $x=0$ 또는 $x=1$ 을 근으로 가지고, 그래프로 나타내면 다음과 같아요.
삼차항의 계수가 음수이므로 삼차함수의 모양도 오른쪽 아래롤 향하는 모양입니다.

극댓값과 극솟값을 구한 다음, 좌표펴면 위에 나타내면,
$f(x)=-x^4+2x^2-3$ 이므로
$f(-1)=(-1)^4+2(-1)^2-3=1+2-3=0$
$f(0)=-3$
$f(1)=-1+2-3=-2$
이제 사차함수의 그래프를 좌표평면 위에 적절한 위치에 놓은 후, 정의역 구간에서 최댓값과 최솟값을 구하겠습니다.

정의역 구간이 $[-1,2]$이므로
최솟값은 $f(0)$의 값과 $f(2)$의 값 중에 어느 값인지 구해야 합니다.
$f(x)=-x^4+2x^2-3$ 이므로
$f(0)=-3$
$f(2)=-16+8-3=-11$
최솟값은 $-11$
이렇게 사파함수의 개형 4가지를 정리하고, 사차함수의 최댓값과 최솟값을 구하는 문제를 풀어보았습니다.
위와 같은 유형의 문제를 무제한으로 생성하고 프린트할 수 있는 혁신적인 학습도구를 소개할까합니다.
'모두매쓰'는 초중고 수학 문제를 유형별로 무제한 생성하는 인공지능 서비스입니다.
위 문제를 충분히 연습하신다면, 수학II의 미적분 실력이 많이 향상될거라 생각합니다.
그럼 오늘도 좋은 하루되세요.
[모두매쓰 생성 연습문제]
고등 수학II > 도함수의 활용 > 사차함수의 최댓값과 최솟값 구하기 연습문제 프린트 학습지
'고등 수학 프린트' 카테고리의 다른 글
| 고등 수학(상) > 이차부등식 > 이차부등식의 해 구하기 연습문제 프린트 학습지 (0) | 2024.07.30 |
|---|---|
| 고등 수학II > 도함수의 활용 > 삼차함수의 최댓값과 최솟값 구하기 연습문제 프린트 학습지 (0) | 2024.07.28 |
| 고등 수학(상) > 다항식의 연산 > 대표적인 곱셈공식의 변형 연습문제 프린트 학습지 (0) | 2024.07.26 |
| 고등 수학(상) > 다항식의 계산 > 곱셈공식 효율적으로 외우기, 개념 연습문제 프린트 학습지 (0) | 2024.07.25 |
| 고등 수학II > 미분법 > 도함수의 정의와 미분법 공식, 연습문제 프린트 학습지 (0) | 2024.07.12 |





